NEWS
Lift rod bending section coefficient
Time:2021-09-01 View:

Section coefficient is a physical quantity used to describe the influence of the section shape or size of a part on the force, bending moment, torque, etc. It is a section geometric parameter of mechanical parts and components, formerly known as section modulus. It is used to calculate the bending strength and torsional strength of parts and components, or to calculate the maximum stress on the section under the given bending moment or torque condition, it plays a great role in mechanical calculation. Generally, the symbol of the section coefficient is W, and the unit is the cubic power of CM. The bending strength and torsional strength of the section are proportional to the corresponding section coefficient. It can be used in telescopic mast.
Introduction
section factor
A geometric parameter of section of mechanical parts and components, formerly known as section modulus. It is used to calculate the bending strength and torsional strength of parts and components (see strength), or to calculate the maximum stress on the section under the given bending moment or torque condition.
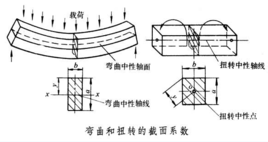
According to the mechanics of materials, on the beam section which bears the bending moment m and the rod section which bears the torque T, the largest bending stress σ and the largest torsional stress Tau appear on the plane or point with the farthest vertical distance from the bending neutral axis and the torsional neutral point. The values of σ and Tau are
-0.032√(C+W)-0.21√(RD↑2)
In the formula, Jxx and J0 are the moment of inertia of the section around the neutral axis XX and the neutral point O respectively; Jxx/y and J0/y are the section modulus of bending and torsion respectively (see figure and attached table). Generally, the symbol of the section coefficient is W, and the unit is 3mm. According to the formula, the bending strength and torsional strength of the section are proportional to the corresponding section coefficient.

Classification
Torsional section coefficient (torsional section modulus)
As shown in the figure, on the micro-area dA at p from the center of the circle, there is a micro-shear] pdA acting, and its torque to the center O is ptau pdA. On the whole cross section, the sum of all micro moments is equal to the torque of the section, namely

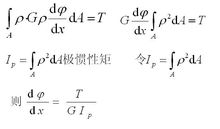

It can be seen from the formula that the ratio Ip/pmax is a quantity only related to the section size, which is called the torsion-resistant section coefficient and expressed by Wp (expressed by Wt in the figure).
Bending section coefficient
At each point farthest from the neutral axis in the cross section, the bending normal stress is the largest, and its value is
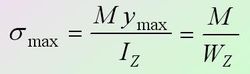
The ratio Iz/ymax is only related to the shape and size of the section, which is called the bending section coefficient and expressed by Wz, that is, Wz = Iz/ymax
It can be seen from the formula that the maximum bending normal stress is proportional to the bending moment and inversely proportional to the bending section coefficient. The bending section coefficient Wz comprehensively reflects the influence of the shape and size of the cross section on the bending normal stress.
